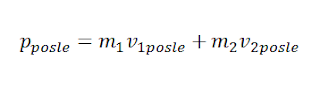Равнотежа тела - полуга

Полуга је чврсти објекат (најчешће нека греда, даска, штап, кључ) који се користи за појачање силе примењене на други објект, уз употребу ослонца.
Полугом се мала сила која делује на дужем путу, претвара у велику силу на краћем путу

Полуге се користе кад је потребно имати велику силу на једном краћем крају полуге (на пример - за подизање тешког објекта), а једино мала сила је на располагању на другом дужем крају полуге

Треба напоменути да се с тим не постиже „чаробно“ повећање расположиве енергије, јер производ (сила*пут) остаје исти - момент силе на оба краја полуге је исти!

Прво испитивање својстава полуге се приписује Архимеду, који је по сазнању свога открића, по легенди рекао: „Дајте ми тачку ослонца, и померићу Земљу“.

Тело је у равнотежи када је збир сила које делују на њега и збир момената сила које делују на њега једнак нули.
Полуга се налази у равнотежи када је разлика у моменту сила које дјелују на њу једнака нули. То значи да је:

Извори:
1. https://sr.wikipedia.org/wiki/%D0%A1%D1%83%D0%B4%D0%B0%D1%80%D0%B8

Сударни процеси и описивање кретања законима одржања

Судар је изолован догађај у којем два или више тела делују силом једно на друго у релативно кратком временском интервалу.
Ако је систем изолован, важи закон одржања импулса, значи - важи и за сударе.
Кинетичка енергија система тела се не одржава, осим ако су судари тела апсолутно еластични. 
Пошто се импулс одржава, закон одржања импулса обично се користи да би се израчунале (предвиделе) брзине тела након судара.

Постоје две основне врсте судара, при чему обе ове врсте конзервишу (одржавају) импулс, а то су:

• Еластични судари у којима се одржава кинетичка енергија и укупан импулс тела пре и после судара
• Нееластични судари у којима се не одржава кинетичка енергија, али је укупан импулс одржан пре и после судара.

Еластични судар је судар у коме не постоји губитак кинетичке енергије. У реалности, при сваком макроскопском судару међу телима ће се изгубити део кинетичке енергије на стварање унутрашње и још неких других облика енергије. Међутим, неки проблеми су довољно близу томе да се могу апроксимирати потпуно еластичним сударом.

Судар између две билијарске кугле је добар пример за скоро потпуно еластични судар.

Импулс две кугле пре судара је једнак импуслу само беле кугле која се креће:

Импулс две кугле после судара, када се обе крећу је једнак збиру импулса беле и обојене кугле:

Како важи закон одржања импулса, импулс пре и импулс после су једнаки, па одатле добијамо:

Брзине кугли су, након судара, мање него брзина беле кугле пре судара.

Нееластичан судар је судар у коме се део кинетичке енергије пређе у неки други облик енергије. Иако због тога не важи закон одржања енергије, код нееластичних судара је одржан импулс. 


Пример нееластичног судара могао би да буде судар две грудве снега које се сударе и “слепљене” наставе заједно да се крећу после тога. 

Овај се слепио за зид 

Следећа једначина описује одржање импулса код нееластичних судара:

Извори:
1. https://sr.wikipedia.org/wiki/%D0%A1%D1%83%D0%B4%D0%B0%D1%80%D0%B8

Релативистичка физика скраћено

Рекапитулција области Релативистичка механика

• Апсолутно црно тело је физички модел идеалног тела које апсорбује све упадно електромагнетно зрачење, без обзира на фреквенцију или упадни угао уз то одржавајући топлотну равнотежу.
• Идеално црно тело не постоји, али га може прилично добро заменити шупљина са малим отвором која је толико непрозирна да једва одбија зрачење:

• Свако тело или материја емитује електромагнетно зрачење када му је температура изнад апсолутне нуле.
• На основу објашњења класичне физике емисиона моћ зрачења апсолутно црног тела у области краћих таласних дужина тежи бесконачности, што није у складу са експерименталним резултатима и законом о одржању енергије. Тај парадокс је популарно назван “ултравиолетна катастрофа“.
• Макс Планк је 1900. године увео претпоставку да се електромагнетно зрачење емитује у облику одвојених количина (порција) енергије – кванта енергије. Значи енергија се емитује дисконтинуално, са прекидима, у пакетима енергије. 
• Енергија једног кванта сразмерна је фреквенцији (f) зрачења:

h универзална Планкова константа

 c брзина светлости

 f и λ су фреквенција и таласна дужина електромагнетног таласа који то тело емитује.

• Фотоефекат (фотоелектрични ефекат) је појава избијања електрона (фотоелектрона) из метала помоћу светлости.
• Минимална енергија коју треба да прими електрон да би напустио површину метала зове се излазни рад (Аi).
• Ову појаву је објаснио Ајнштајн 1905. године, и касније за тај научни рад добио Нобелову награду.
• Фотефекат се дешава када електрон апсорбује један квант енергије и део те енергије потроши на излазни рад (Аi), део може да преда кристалној решетци, а преостали део ће бити кинетичка енергија (Ек) фотоелектрона, по напуштању метала.

hν = Ai + Ek

• У неким случајевима светлост испољава таласна својства (интерференција, дифракција), а у другим  честична својства (фотоефекат).
• Луј Де Брољи је 1924. године изнео претпоставку да дуализам није особина само оптичких појава, већ је универзално својство материје, да све честице поседују и таласна својства.
• Са сваком честицом која има импулс повезан је талас чија је таласна дужина:

• Свака честица која се креће мора да има и таласну дужину. Таласна дужина те честице (Де Брољева таласна дужина) је једнака количнику Планкове константе h и интензитета импулса честице p.
• Хajенбергов принцип неодређености каже да је немогуће истовремено одредити тачан положај и импулс (брзину) неке честице
• Ово није последица несавршености мерних инструмената, него је квантно својство самог посматраног система и немогуће га је избећи и употребом усавршених мерних инструмената (буквално тако функционише природа!)
• Хајзенбергова релација неодређености за импулс и положај:

Δp·Δx ≥ ħ/2

Δp неодређеност импулса

Δx неодређеност положаја

ħ редукована Планкова константа ħ  = h/2π         h=6,626·10 на −34 Js

• Хајзенбергова релација неодређености за енергију и време:

ΔE·Δt  ≥ ħ/2

ΔE неодређеност енергије

Δt неодређеност мереног временског интервала 

Извори:

https://sr.wikipedia.org/wiki/%D0%90%D0%BF%D1%81%D0%BE%D0%BB%D1%83%D1%82%D0%BD%D0%BE_%D1%86%D1%80%D0%BD%D0%BE_%D1%82%D0%B5%D0%BB%D0%BE

https://fizis.rs/

http://kluszeljka1.weebly.com/fotoelektri269ni-efekat.html

https://bs.wikipedia.org/wiki/Heisenbergov_princip_neodre%C4%91enosti

Термодинамика скраћено

Рекапитулација области Термодинамика

• Унутрашња енергија зависи од структуре и термодинамичког стања тела, а представља збир укупне енергије његових саставних честица. 
• Унутрашњу енергију система не чини кинетичка енергија кретања система као целине, нити потенцијална енергија система услед положаја.
• Унутрашња енергија се не мери директно, већ се мери промена унутрашње енергије ΔQ. 
• Топлота прелази са тела које има вишу температуру на тело ниже температуре 

• Пренос топлоте се врши на један од следећих начина:

1. Директним провођењем (кондукција)
2. Зрачењем (радијација)
3. Посредним превођењем (конвекција)

• Eнергијa коју тело прими или отпусти у процесу топлотне размене назива се количина топлоте.
• Топлотна размена је процес преношења енергије између система и околине због разлике у температури, без вршења рада.
• Количина топлоте зависи од промене температуре, масе и врсте супстанције на следећи начин:

Q=mcΔT

Q – количина топлоте (као и друге врсте енергије мери се џулима J)

m – маса

c – специфични топлотни капацитет

ΔT – промена температуре

Т је термодинамичка температура и изражава се у келвинима К

• Количина топлоте коју тело прима при загревању или отпушта при хлађењу зависи од масе тог тела, од специфичног топлотног капацитета супстанције и од промене температуре.
• Специфични топлотни капацитет супстанције (с) је бројно једнак количини топлоте која је потребна за загревање 1kg те супстанције за 1К.
• Ако нема размене топлоте кажемо да су систем и околина у топлотној равнотежи.
• Количина топлоте која се пренесе провођењем кроз раван хомоген зид 

је пропорционална:

 површини преко које се преноси (S),

 коефицијенту топлотне проводљивости (λ),

 температурној разлици (T)

 времену (t), 

а обрнуто пропорционална дебљини зида (d):

• Први принцип термодинамике гласи: Количина топлоте, доведена изолованом систему, може једним делом да повећа његову унутрашњу енергију, а други део може да се претвори у рад тог система.
• Перпетуум мобиле прве врсте је машина која би бесконачно дуго вршила користан рад без утрошака енергије. То значи да би ова машина могла да ствара себи енергију за рад вршећи рад, а не трошећи своју унутрашњу енергију. Према првом закону термодинамике и закону одржања енергије, конструисање овакве машине није могуће.
• Други принцип термодинамике, Клаузијусово начело: Ентропија изолованог система није равнотежна, већ временом тежи да се приближи маскимуму. Укупна ентропија изолованог система се никада не може смањити током времена
• Перпетуум мобиле друге врсте је машина која би потпуно претворила топлоту у користан рад, а да овој машини не треба хладњак (тело са нижом температуром). Не постоји могућност претварање целокупне топлоте у користан рад без губитака енергије, па тиме ни конструисање овакве машине није могуће. 

Извори:

https://sr.wikipedia.org/sr-ec/Unutra%C5%A1nja_energija

https://fizis.rs

http://www.ingkomora.org.rs/strucniispiti/download/ee/TP5-1_Uslovi_gradjevinske_fizike.pdf

https://sr.wikipedia.org

Sferna ogledala

Do sada je već bilo reči o ravnim ogledalima.
Sferna ogledala su poseban slučaj zakrivljenih ogledala i sa njima se učenici prvi put sreću u osmom razredu osnovne škole u okviru oblasti optika.
Sferna ogledala su posebna po tome što je kod njih, površina o koju se odbija svetlost, deo sfere.
Sfera  je površ čije su sve tačke jednako udaljene od centra.
Na primer, površina lopte je sfera.
Da bismo bolje objasnili kako to izgleda ispupčeno (konveksno) i udubljeno (konkavno) ogledalo, uzmimo za primer predmet koji svi imamo u kući - kutlača. Ako je lepo uglačana, spoljašnja površina kutlače predstavlja konveksno, a unutrašnja površina kutlače (ona u koju ide supa) predstavlja jedno konkavno ogledalo.
U školi se uči konstrukcija likova kod sfernih ogledala na primerima ogledala čija je zakrivljenost mala, tj. njihova površina je samo jedan mali deo sfere, tako da bez problema mogu da se primene karakteristični zraci prilikom konstrukcije lika nekog predmeta.

Pre nego što pređemo na karakteristične zrake, upoznajmo se sa pojmovima koji će nam biti potrebni:
Optička osa: prava linija koja je u pravcu radijusa (poluprečnika) sfere. Prolazi kroz centar i teme ogledala.
Centar: tačka koja predstavlja centar sfere čiji je deo naše sferno ogledalo.
Teme: Tačka u kojoj se seku optička osa i ogledalo.

Žiža (fokus): Tačka u kojoj se seku odbijeni zraci koji su do ogledala došli paralelno optičkoj osi, kod konkavnog ogledala, a kod konveksnog, tačka u kojoj se seku produžeci zraka koji su do ogledala došili paralelno optičkoj osi.

Postoje četiri karakteristična zraka koja se koriste za konstrukciju lika predmeta, mada je za konstrukciju dovoljno odabrati samo dva od ova četiri. Karakteristični zraci su u suštini isti i za konkavna i za konveksna ogledala, s tim što je žiža (fokus) kod konkavnog ogledala imaginarna - nalazi se sa druge strane ogledala.

Karakteristični zraci:
1. Kreće se paralelno optičkoj osi i posle odbijanja prolazi kroz žižu (F).
2. Prolazi kroz žižu (F) i odbija se paralelno optičkoj osi.
3. Prolazi kroz centar (C) i posle odbijanjanja se vraća nazad po istoj putanji.
4. Pada u teme (T) i odbija se pod istim uglom u odnosu na optičku osu pod kojim je pao na ogledalo. Ovaj karakteristični zrak je teži za konstrukciju od ostalih, pa se retko koristi i nije dat na donjoj slici.

Nadam se da vam je objašnjenje bilo od pomoći. 

Ako ima pitanja, predloga itd, pišite u komentarima da bismo mogli da razgovaramo o tome.

Masa i težina - računanje

Ako znamo masu nekog tela, lako možemo da izračunamo njegovu težinu i obratno, ako znamo težinu, lako možemo da izračunamo masu.
Pritom, uvek treba imati na umu da su masa i težina dve različite stvari:
Masa je mera inertnosti tela.
Težina je sila kojom telo pritiska podlogu ili zateže kanap o koji je obešeno.
Formule koje se koriste pri računanju su, zapravo, direktna primena drugog Njutnovog zakona.

Formula koja se koristi kada računamo težinu nekog tela na Zemlji, a znamo njegovu masu je:

Q = mg

Gde je
Q - težina
m - masa
g - gravitaciona konstanta (u ovom slučaju je Zemlja u pitanju pa je g = 9.81m/s2)

Primer:
Moja masa je 60kg, a težinu računamo kao:
Q = 60kg*9.81m/s2
Q = 588.6N
Pošto je težina sila njena jedinica je N - njutn.

Formula koja se koristi kada računamo masu nekog tela na Zemlji, a znamo njegovu težinu je:

m = Q/g

Oznake su iste kao i u gornjoj formuli.

Primer:
Prilikom merenja nekog predmeta, dinamometar pokazuje vrednost od 100N. Njegovu masu računamo kao:
m = 100N/9.81m/s2
m = 10.19kg

Nadam se da vam je ovo bilo od pomoći.
Ako imate pitanja ili predloge, pišite u komentarima da bismo mogli da razgovaramo o tome.

Treći Njutnov zakon - definicija, primeri

Treći Njutnov zakon je poznat i kao Zakon akcije i reakcije". Ovaj zakon se u školi prvi put uči u sedmom razredu.
Logično, svaka akcija ima svoju reakciju. U udžbenicima za fiziku se to malo drugačije kaže.

Definicija: Sila akcije jednaka je sili reakcije po intenzitetu, imaju isti pravac, a smer im je suprotan.

U osnovnoj školi se vektori ne obrađuju, samo se pominje koje su veličine vektorske a koje skalarne.
Sila je vektorska veličina, pa zbog toga je određena pravcem, smerom i intenzitetom.
Sile akcije i reakcije deluju na istom pravcu (pravac je zamišljena prava linija), imaju isti intenzitet (istu brojnu vrednost), a smer im je suprotan (jedna na jednu stranu, a druga na suprotnu), ili kako ja volim da kažem: "jedna deluje natam, a druga navam".

Formula kojom se izražava ovaj zakon, izgleda ovako:

     Fa = Fr

Ili ako se prilikom pisanja koriste vektori:

Minus u gornjoj formuli označava upravo to da sile deluju u suprotnim pravcima!

Ovaj zakon, kao i prvi Njutnov zakon, je široko primenljiv i to ne samo u fizici.
Primeri:
1. Kada ja rukom pritisnem sto celom svojom težinom (težina je sila!) od oko 600N (kako računamo težinu ako znamo masu, možete pogledati ovde) i sto, ukoliko se ne slomi, deluje na moju ruku istom silom suprotnog smera.
2. Kada ljudi obaraju ruke, u toku borbe, dok se takmičari još uvek muče ko će koga da nadvlada, ruke im se ne pomeraju jer jedna ruka na drugu deluje istom silom, u istom pravcu ali suprotnog smera.
3. Ovaj primer nije primenljiv u osnovnoj školi, ali je interesantan za razmatranje: kada se kuglica kreće po strmoj ravni, ako zanemarimo trenje između kuglice i ravni, na nju deluje samo gravitaciona sila, ali ta sila, pošto deluje normalno na podlogu, a na ravan pod nekim uglom, sila gravitacije se razlaže na 2 komponente: prva je paralelna sa strmom ravni i ona se koristi u proračunima, a druga je normalna na podlogu i ona biva poništena silom reakcije podloge!

Nadam se da vam je ovaj tekst bio od pomoći.
Ukoliko imate pitanja ili predloge, pišite u komentarima da bismo mogli da razgovaramo o tome.